FlashAttention 2 原理 | 深度学习算法
FlashAttention 2 在 FlashAttention 的基础上进行了进一步的性能优化,其计算结果仍然是严格对齐的。本文仅包含对 FlashAttention 2 在前向推理上的优化,不包含反向传播相关内容。
减少 non-matmul 操作
虽然 non-matmul 操作的计算量仅占总计算量的一小部分,但它们的执行时间较长,这是因为 GPU 有专用的矩阵乘法计算单元,其吞吐量比非矩阵乘法吞吐量要高。
rescale
首先回顾一下 FlashAttention 的分块计算流程:
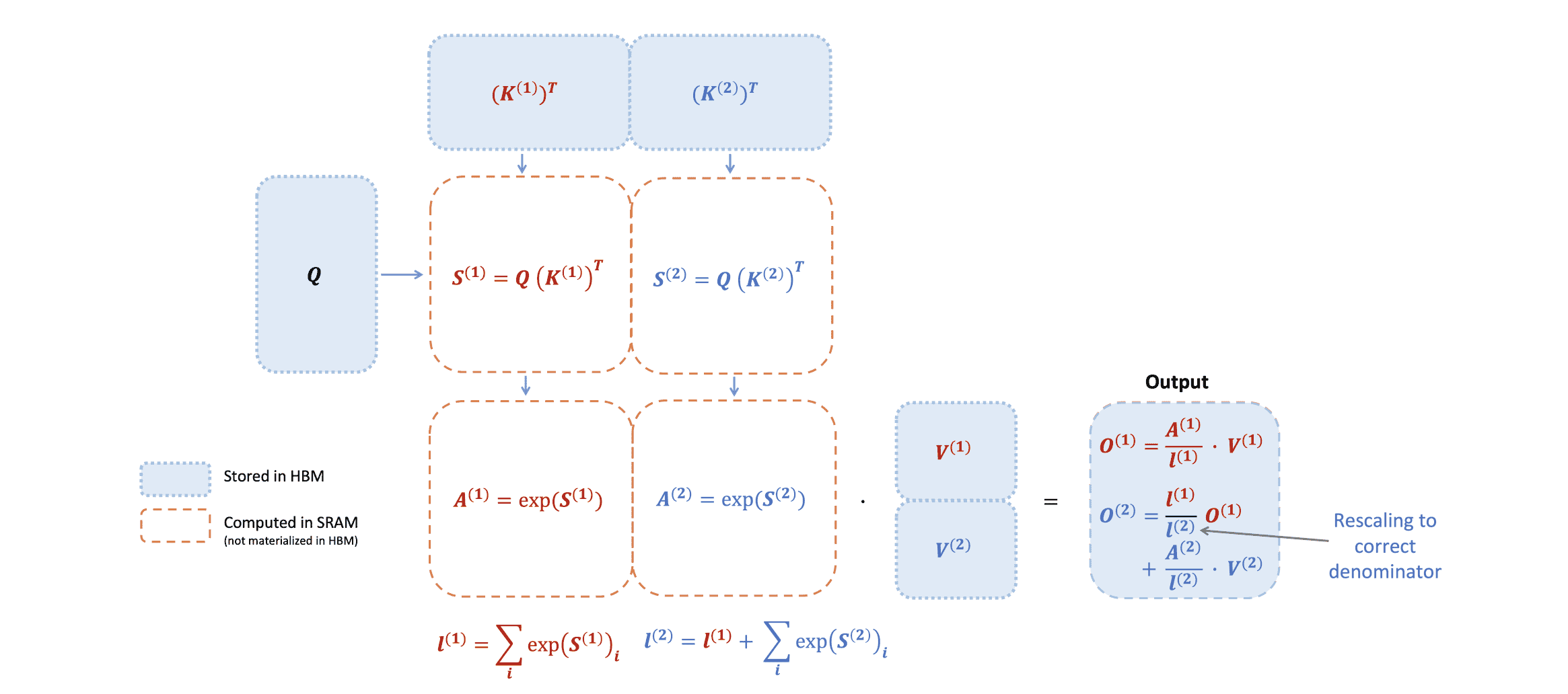
FlashAttention 的计算步骤(红框部分为 FlashAttention 和 FlashAttention 2 不同的地方):
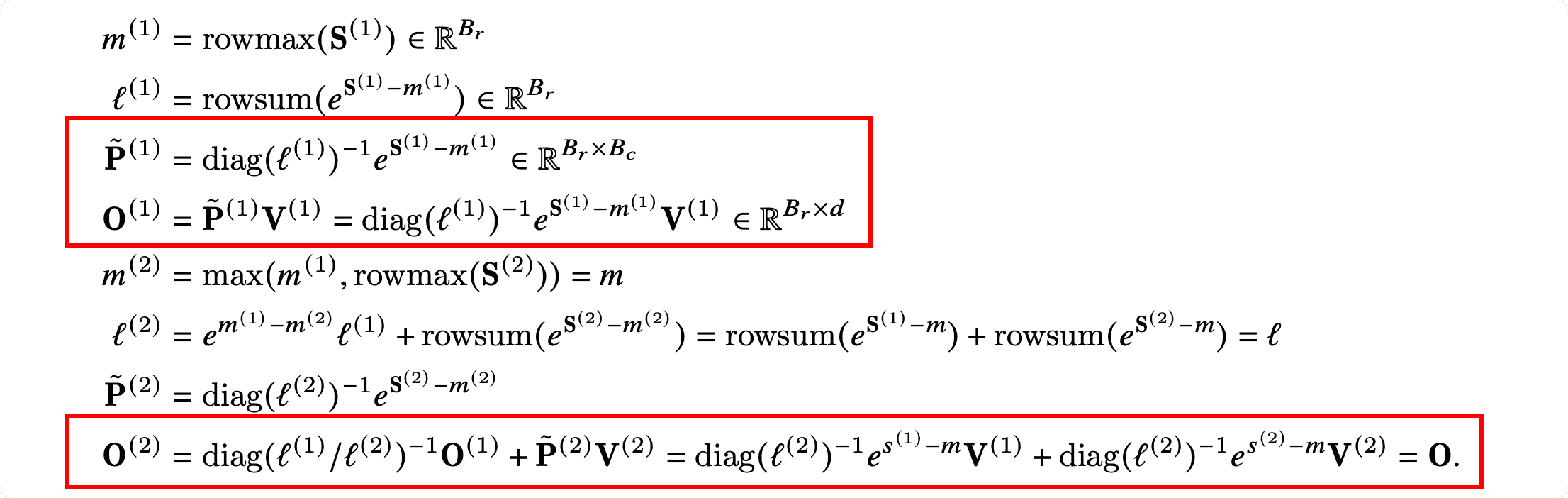
- 在计算局部 attention 时,FlashAttention 2 先不考虑 softmax 的分母 $l^{(i)}=\sum e^{x_i}$,即:
- FlashAttention:$\mathbf{O}^{(1)}=\mathbf{\tilde{P}}(1)\mathbf{V}^{(1)}=\mathrm{diag}\left(\ell^{(1)}\right)^{-1}e^{\mathbf{S}^{(1)}-m^{(1)}}\mathbf{V}^{(1)}$
- FlashAttention 2:$\mathbf{O}^{(1)}=e^{\mathbf{S}^{(1)}-m^{(1)}}\mathbf{V}^{(1)}$
- 在更新 $O$ 时不需要对 $l^{(i)}$ 进行 rescale:
- FlashAttention:$\mathbf{O}^{(2)}=\mathrm{diag}\left(\ell^{(1)}/\ell^{(2)}\right)^{-1}\mathbf{O}^{(1)}+\mathrm{diag}\left(\ell^{(2)}\right)^{-1}e^{\mathbf{S}^{(2)}-m^{(2)}}\mathbf{V}^{(2)}$
- FlashAttention 2:$\mathbf{\tilde{O}}^{(2)}=\mathrm{diag}\left(e^{m^{(1)}-m^{(2)}}\right)\mathbf{\tilde{O}}^{(1)}+e^{\mathbf{S}^{(2)}-m^{(2)}}\mathbf{V}^{(2)}=e^{s^{(1)}-m}\mathbf{V}^{(1)}+e^{s^{(2)}-m}\mathbf{V}^{(2)}$
- 在整个循环的最后,需要将 $\mathbf{\tilde{O}}^{(\mathrm{last})}$ 更新成 $\mathbf{O}$:
- $\mathbf{O}=\mathrm{diag}\left(\ell^{(\mathrm{last})}\right)^{-1}\mathbf{\tilde{O}}^{(\mathrm{last})}$
这个更新过程可以描述成这样:
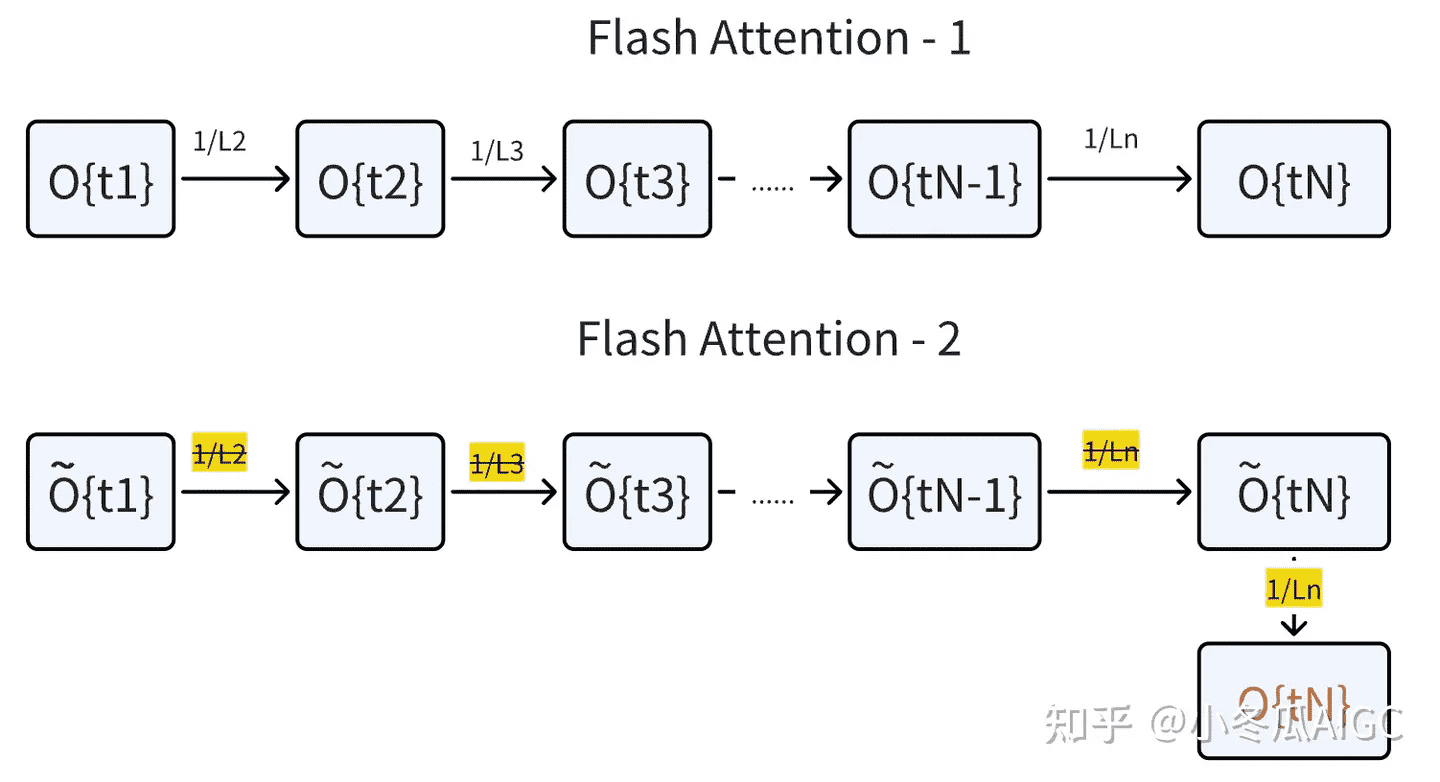
FlashAttention 2 的计算步骤(红框部分为 FlashAttention 和 FlashAttention 2 不同的地方):
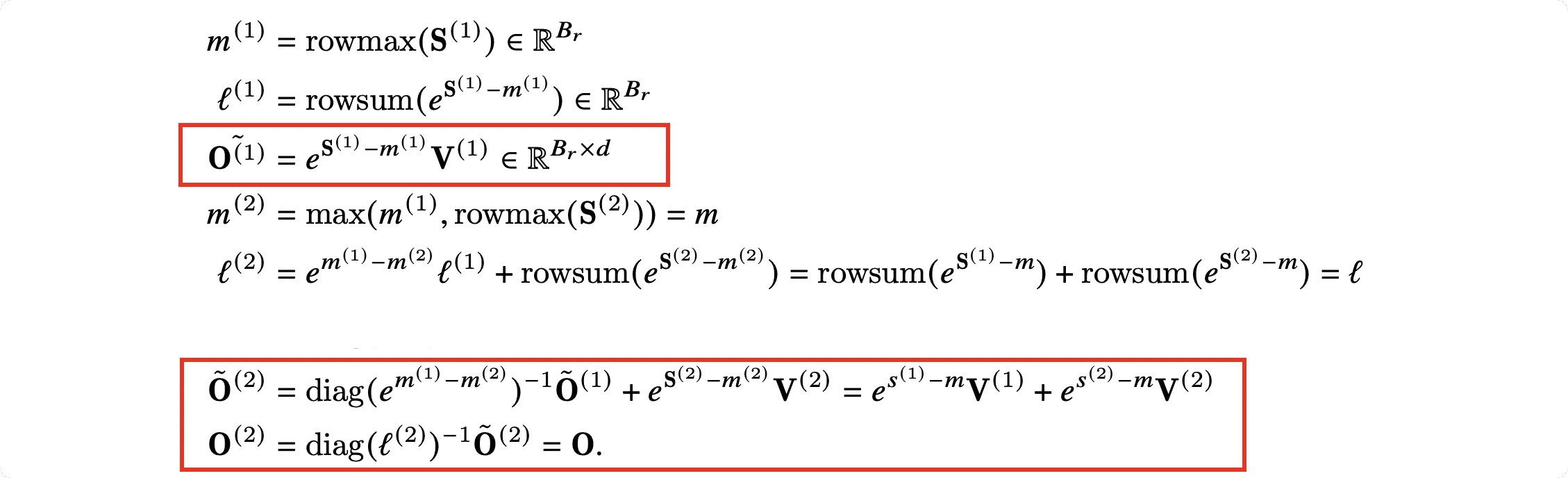
现在再看下原论文中的伪代码就比较容易理解了:

causal masking
因果掩码(causal masking)是 attention 的一个常见操作,特别是在自回归语言模型中,需要对注意力矩阵 S 应用因果掩码。由于 FlashAttention 和 FlashAttention 2 已经通过块操作来实现,所有列索引都大于行索引的块(大约占总块数的一半)的计算都可以被跳过。
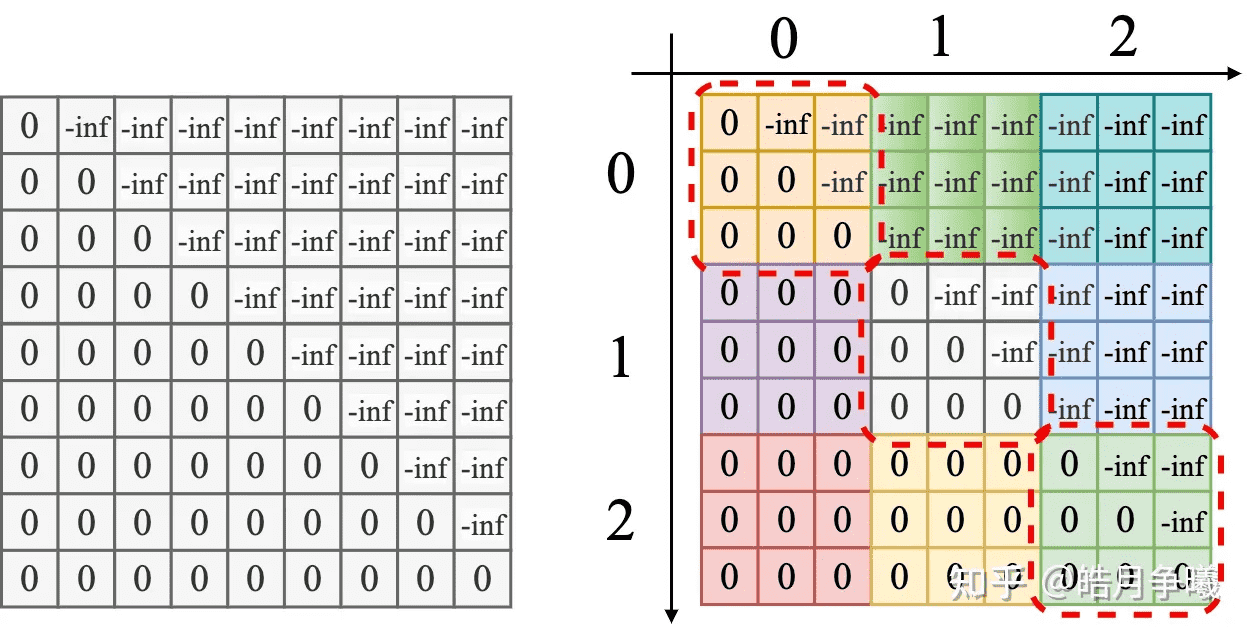
如上图左图所示,由于整个右上三角都是 -inf 值,经过 softmax 都会变成接近 0 的数,对应这部分的数据可以不用计算,从而达到节省计算量和 IO的效果。上图右图中 9 个 block 的区域可以分成 3 类,对角线区域(红色框)、对角线右上区域、对角线左下区域,右上区域不用计算,左下区域直接计算不用加 mask,对于中间对角线区域需要加 mask,但是 mask 是一致的,也就是说在实际的处理中可以统一处理,不会产生分支,并且只需要处理一次就可以了。
在序列长度维度上并行化
在 FlashAttention 中,只在两个维度上进行了并行化:
- 不同 batch 之间是并行的:可以理解成 Q 的每 n 行是一组(n 就是 batch size),每组之间的计算是并行的
- 不同 head 之间是并行的:前面的示意图都只展示了一个注意力头,所以可以理解成有多个示意图描述的计算是并行的
使用一个 thread block 来处理一个注意力头,总共需要 block 的数量为 batch_size * head_number。每个 block 被调度到到一个 SM 上运行。当需要的 block 数量很大时,这种调度方式是高效的,因为几乎可以有效利用 GPU 上所有计算资源。
但是在处理长序列输入时,由于内存限制,通常会减小 batch size 和 head 数量,这样并行化程度就降低了。因此,FlashAttention 2 还在序列长度这一维度上进行并行化。同时因为 Q 的每一行是独立的,不需要信息交互,所以可以利用这个特性将它们并行化。
FlashAttention 2 的另一个改进是将内外层循环的顺序调换了,这样做是为了把 Q 的分块移到外层进行 block 级别的并行(在序列长度维度上并行),可以理解成每 $B_r$ 条样本是一组,每组之间的计算是并行的。
注意这里 FlashAttention 的外层循环(FlashAttention 2 的内层循环)只能串行计算,因为这个方向的计算依赖上一次迭代的结果。
优化 warp 级别调度
接下来看 block 内部的 warp 之间是如何进行调度的:
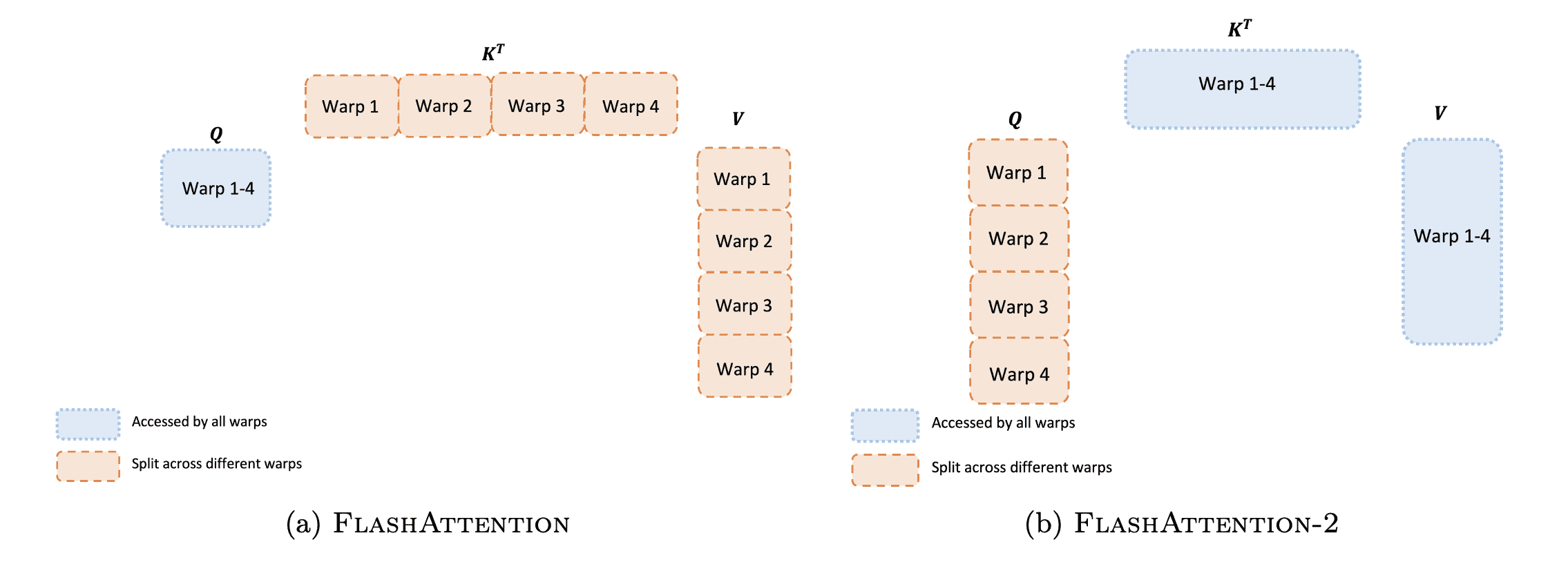
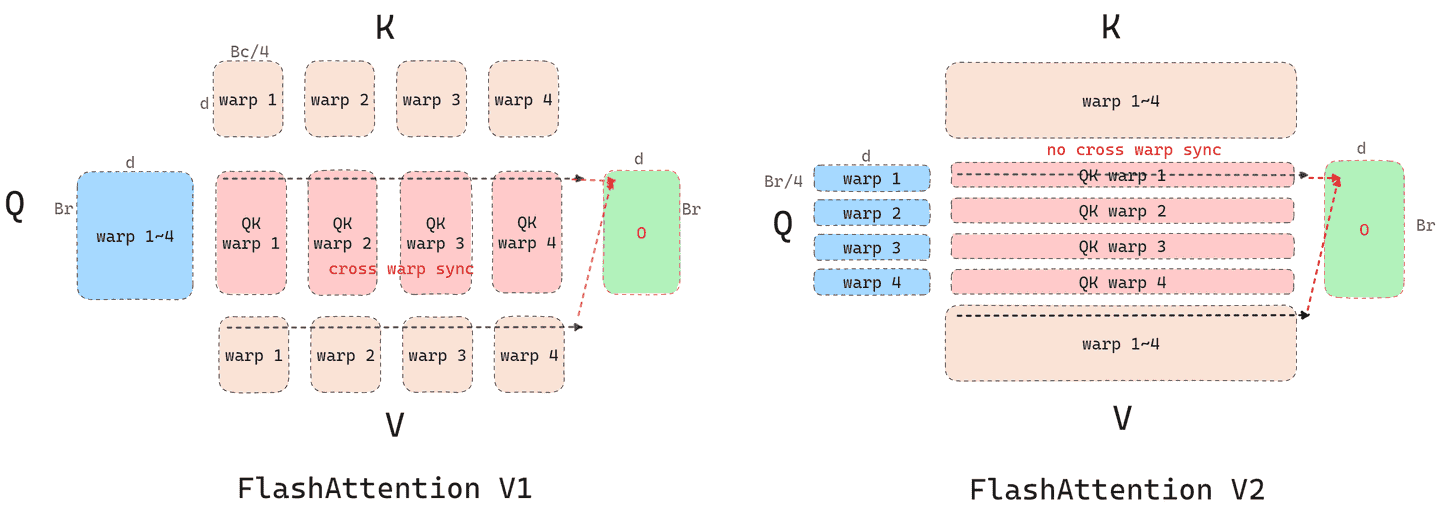
FlashAttention 采用了 split-K 方案:
- 将 K 和 V 划分成 4 个 warp,而 Q 对所有 warp 可见
- 每个 warp 对应的 K 分块和 Q 进行乘法,得到 QK 的一个分块
- 每个 warp 对应的 QK 分块和对应的 V 分块进行矩阵乘法(这里省略了对 softmax 过程的叙述),得到 QKV 分块
- 所有 warp 需要通信,将 QKV 分块写到共享内存,再相加得到最终输出 O 的一部分
这个方案的缺点是需要大量的共享内存读写操作和 warp 之间的同步降低了效率。
而 FlashAttention-2 改为了 split-Q 方案:
- 将 Q 划分成 4 个 warp,K 和 V 对所有 warp 可见
- 每个 warp 对应的 K 分块和 Q 进行乘法,得到 QK 的一个分块
- 每个 warp 对应的 QK 分块和对应的 V 分块进行矩阵乘法(这里省略了对 softmax 过程的叙述),直接得到最终输出 O 的一部分,不需要与其他 warp 通信
这个方案可以减少共享内存的读取与写入,也避免了 warp 之间的同步。
这里再贴一个动图,可以更直观的看到计算过程:

参考
FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning
FlashAttention 2 原理 | 深度学习算法