CUDA 实践:隐式 GEMM 卷积 | CUDA
img2col + GEMM 是一种比较常用的卷积优化方法,因为这样可以利用到性能已经优化得比较好的 BLAS 库。早期的一些深度学习框架(如 Caffe)就是用了这种方式。但是这种方式有个弊端,就是需要大量的内存/显存来存储中间结果。隐式 GEMM 卷积则可以直接从原始 feature map 和 weight 中取值,避免产生占用巨大内存/显存的中间结果矩阵。
算法流程
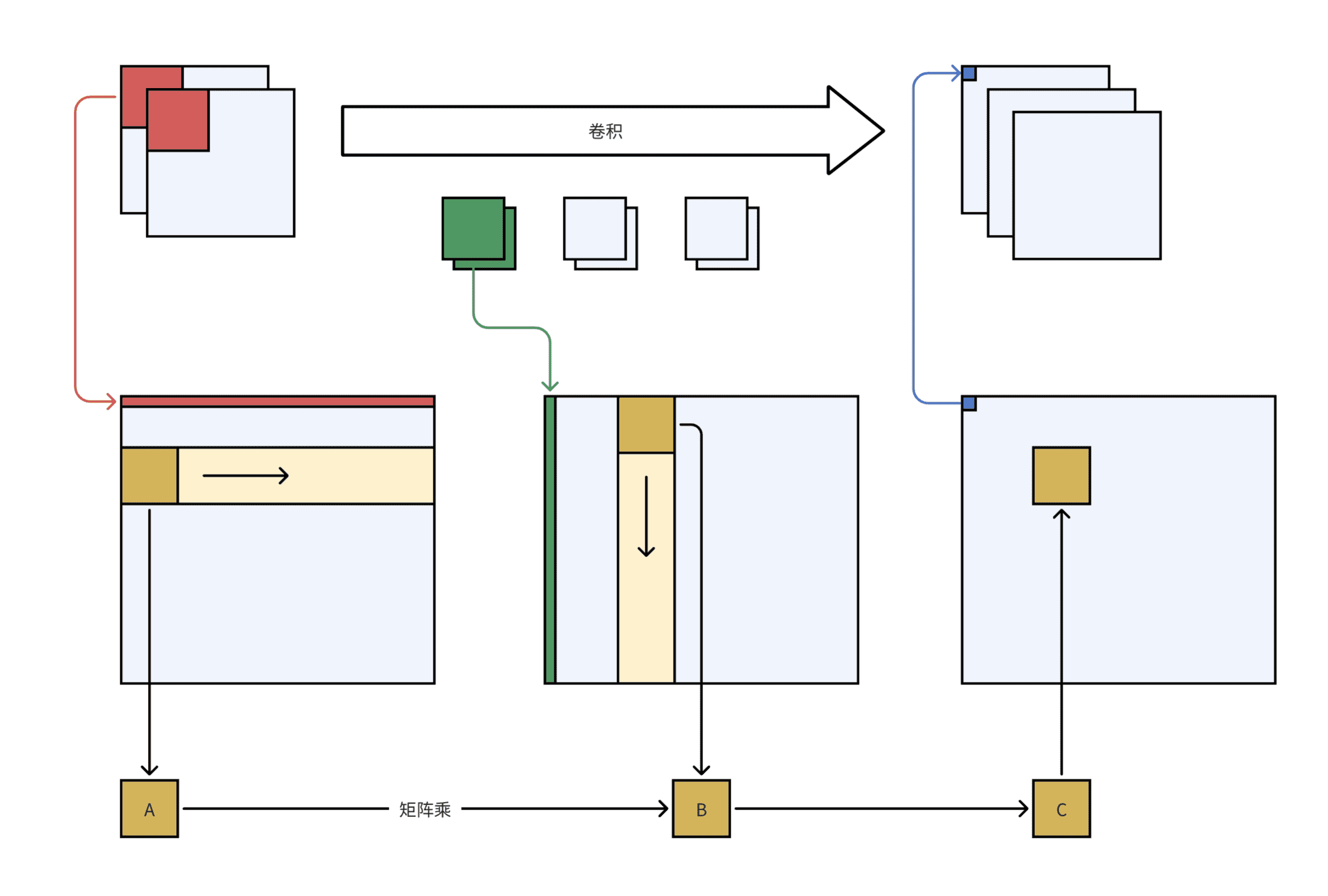
上图的红绿蓝色部分展示了 img2col 的流程,黄色部分展示了分块矩阵乘的流程。可以看出,三个大的中间结果矩阵其实不必实际存在,只需要在构建小矩阵 A、B、C 的时候直接根据计算出的索引从原始的 feature map 和 weight 中取值即可。
在卷积运算中,输入 feature map、weight、输出 feature map 三者都是 4 维的 tensor,形状分别为 [N, IC, IH, IW]、[OC, IC, KH, KW]、[N, OC, OH, OW]。其中输入的元素坐标 ih,iw 和输出的元素坐标 oh,ow,kh,kw 的关系式可以写为:
1 | ih = oh * stride_h - pad_h + kh |
根据 img2col 算法,卷积运算可以转化为矩阵乘法:
1 | C = Matmul(A, B) |
其中:
- 矩阵 A 由输入 feature map 转换而来,是一个尺寸为 [n·OH·OW, IC·KH·KW] 的矩阵(行优先)
- 矩阵 B 由 weight 转化而来,是一个尺寸为 [IC·KH·KW, OC] 的矩阵
- 矩阵 C 可以转换为输出 feature map,是一个尺寸为 [n·OH·OW, OC] 的矩阵
矩阵和 tensor 在各个位置上的元素的对应关系为
$$\begin{gathered}
A_{ik}=\mathrm{x}\left(\mathrm{n},\mathrm{ic},\mathrm{ih},\mathrm{iw}\right) \
B_{kj}=\mathrm{w}\left(\mathrm{oc},\mathrm{ic},\mathrm{kh},\mathrm{kw}\right) \
C_{ij}=\mathrm{y}\left(\mathrm{n},\mathrm{oc},\mathrm{oh},\mathrm{ow}\right)
\end{gathered}$$
其中矩阵的下标 i,j,k 和 tensor 的坐标之间的关系为
1 | i = n * OH * OW + oh * OW + ow |
当 i 已知时,可以用下面的关系式推算出输出 feature map 的坐标:
1 | n = i / (OH * OW) |
当 k 已知时,可以推算出 weight 的坐标:
1 | ic = k / (KH * KW) |
同时结合 oh,ow,kh,kw,就可以计算出 ih 和 iw。这样就能根据 A 矩阵中的坐标反推输入 feature map 中的坐标。
根据上面的推导,卷积的运算过程可以写成一个隐式矩阵乘法的形式:
1 | GEMM_M = N * OH * OW |
上面的隐式矩阵乘法算法仍然是串行的形式,接下来对整个计算任务进行分块,让每个 warp 负责拷贝数据到共享内存,并计算得到尺寸为 [WMMA_M, WMMA_N] 的结果矩阵:
1 | def do_conv(i, j): |
代码实现
在本文的实现中,我们用到了 tensor core 来完成小矩阵的乘法运算(即上一节图中的 A、B、C)。CUDA C++ 中包装了 tensor core 的 API(使用方法可以参考官方文档),在 nvcuda::wmma 命名空间下。这里的 wmma 是 warp matrix multiply accumulate 的缩写,从名字可以看出,tensor core 的矩阵乘法是以 warp 为单位进行的。所以不同于之前的 CUDA 程序以线程粒度考虑问题,这次我们以 warp 粒度考虑问题。在实际实现中,每个线程块由 (2, 128) 线程网格组成,也可以将其视为 (2, 4) warp 网格:

整个计算过程仍然分成三步:1. 将数据搬运到共享内存;2. 完成计算;3. 写回结果到全局内存。
在计算时,每个 warp 完成 16x16 的矩阵乘法(即 A,B,C 三个子矩阵的尺寸都是 16x16),所以每个 warp 需要从输入 feature map 中搬运 16x16 的数据,平均每个线程搬运 8 个。weight 矩阵同理。这里的做法是让前 16 个线程加载第一行 16 个元素,让后 16 个线程加载第二行 16 个元素,然后循环重复此过程 8 次以加载完整图块。
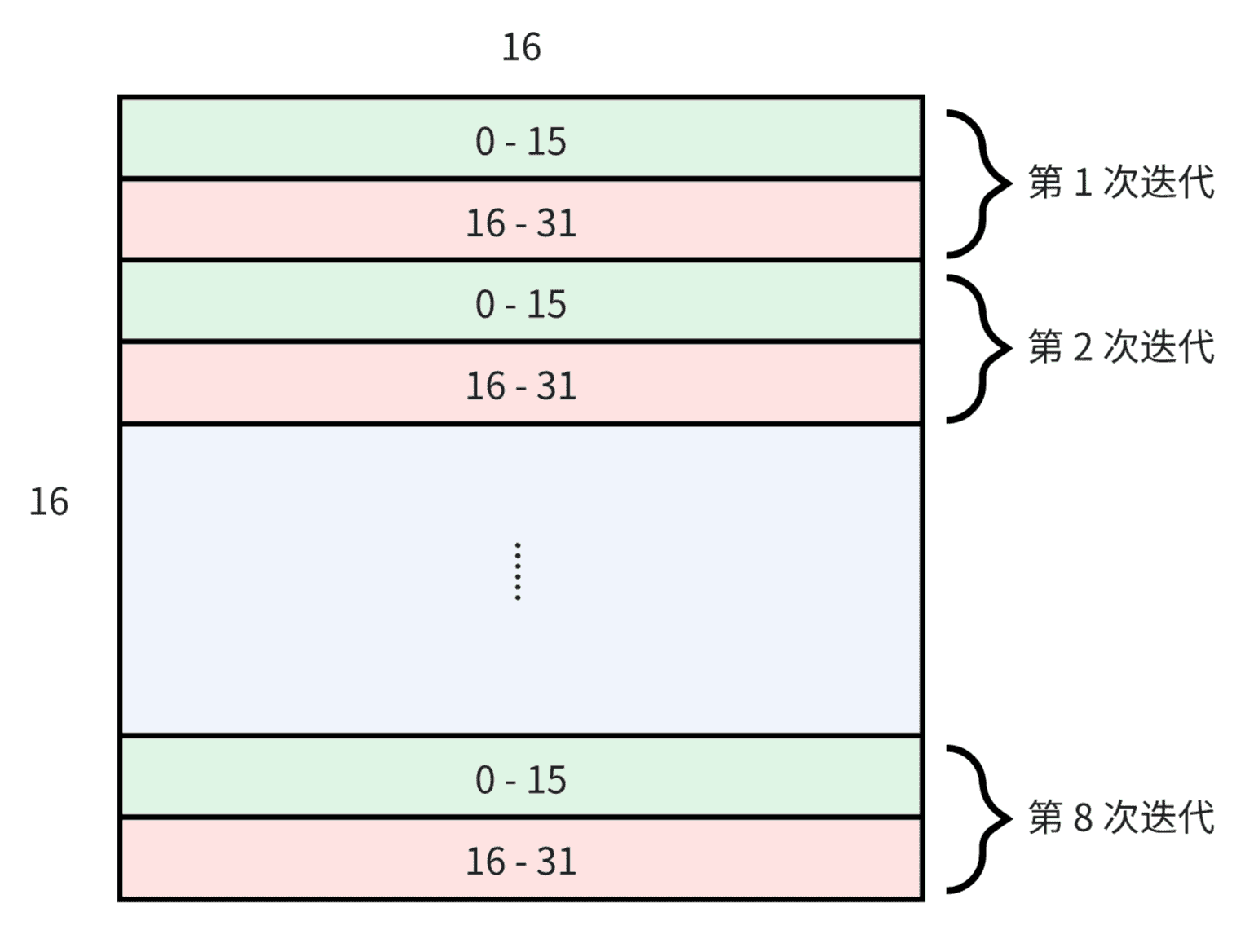
完成数据搬运后再进行子矩阵的乘法即可,最后将结果直接写回全局内存。
完整代码在 zh0ngtian/cuda_learning。
TODO
- 修复某些尺寸下结果不正确的问题
- 优化数据传输:合并访存、异步传输等
参考
ardenma/implicit-gemm-tensor-core-convolution
CUDA 实践:隐式 GEMM 卷积 | CUDA